binary search is prety tricky and have a lot hidden dents, here is my summary.

Common problem

given a non-descending array, find element with value m in the array.

below is the classic c code

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
int binary_search(int *A, int n, int target)
{
    int low = 0, high = n - 1;
    assert(A != NULL && n >= 0);
    while (low <= high)
    {
        int mid = low + (high - low) / 2;
        if(A[mid] == target)
            return mid;
        else if (A[mid] < target)
            low = mid + 1;
        else
            high = mid - 1;
    }
    return -1;
}

there are several places you need to consider, which is shown below : 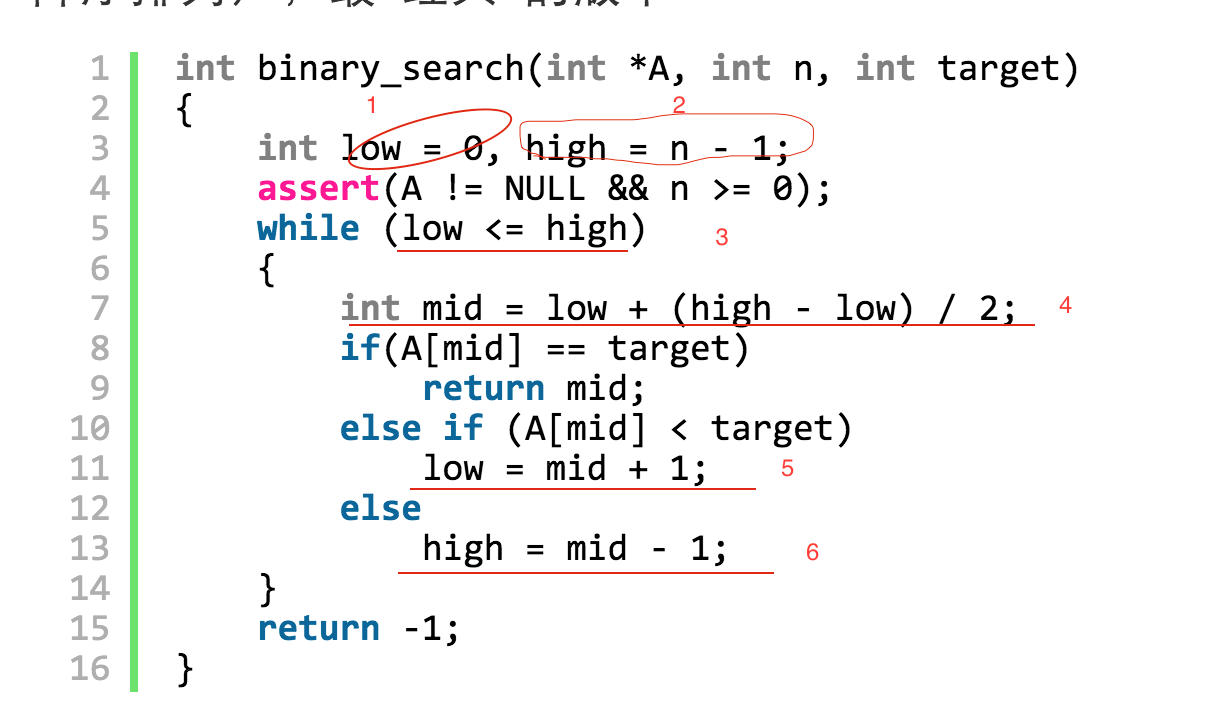bs1
there are totally 6 places you need to be aware whey you write to binary search.

  • for 1 and 2, I choose the close bounary 0 and n-1.

  • for 3, I choose low <= high,why? let’s assume test case [3, 5, 7, 9, 10], assume I search target = 10,

    1. low = 0, mid = 2, high = 5, 10 > a[mid]= 7, so low = 3.
    2. low = 3, mid = 4, high = 5, 10 > a[mid] = 9, so low = 10
    3. if the while loop check is low < high, at this time, the loop would terminate, you didn’t get the new mid and compare it with the target.

  • for place 4, it is also very tricky. Generally, people like to use int mid = (low + high)>>1, but there are some risks there. if low and high is big int, then the sum would possibly overpass the INT_MAX. so it is safe to use the format at place 4. but why not use int mid = high - (high-low) >> 1? In fact, in some case, we have to use it that way.

  • for place 5 and place 6, they have differnet form, you might use low = mid or low = mid+1, for high, it might be high = mid -1 or hign = mid, it is case by case.

basically, all the binary search problem is somehow related to how to find the proper combination for the 6 places. So Here I will give example.

Problem 1

given a sorted(non-ascending) array A, it may contains repeated elements, get the smallest i which make A[i]=target, if not, return -1.

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
int searchFirstPos(int A[], int n, int target)
{
  if(n <= 0) return -1;
  int low = 0, high = n-1;
  while(low < high) // 1 - is low <= high doable?
  {
    int mid = low+((high-low)>>1);
    if(A[mid] < target)
      low = mid+1;
    else // A[mid] >= target
      high = mid; // 2, why not high = mid -1 ?
  }
  /* 
  循环过程中，当low大于0时，A[low-1]是小于target的，因为A[mid] < target时，
  low=mid+1；当high小于n-1时，A[high]是大于等于target的，因为A[mid] >= target时，
  high = mid；循环结束时，low 等于 high，所以，如果A[low](A[high])等于target，
  那么low(high)就是target出现的最小位置，否则target在数组中不存在。
  */
  if(A[low] != target)
    return -1;
  else
    return low;
}

question 1 : at the comment 1, can I use low <= high?
answer : you can not. assume you have array A = [2,2], target = 2, the loop step is like this :

  • low = 0, high = 1, mid = 0.
  • since A[mid] ==target, we got high = mid = 0. at this time, low == high, continue loop.
  • low = 0, high=mid=0 => mid=0, so A[mid]==targt, infinite loop.

see the leet code issue - Search Insert Position

Given a sorted array and a target value, return the index if the target is found. If not, return the index where it would be if it were inserted in order.

You may assume no duplicates in the array.

Here are few examples.

[1,3,5,6], 5 → 2
[1,3,5,6], 2 → 1
[1,3,5,6], 7 → 4
[1,3,5,6], 0 → 0

code : 

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
class Solution {
public:
    int searchInsert(vector<int>& nums, int target) {
        
         if(nums.empty())
        {
            return 0;
        }
        int left = 0;
        int right = nums.size(); // or nums.size()-1, both are fine
        while(left<right)
        {
            int mid = left + floor((right-left)/2);
            if(target > nums[mid])
            {
                left = mid+1;
            }
            else
            {
                right = mid;
            }
        }
        if(left==nums.size()-1&&nums[left]<target)
        {
            return left + 1;
        }
        return left;
        
    }
};

Problem 2

given a sorted(non-descending) array, may contains repeated elements, find the biggest i which makes A[i] = target, if not , return -1.

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
int searchLastPos(int A[], int n, int target)
{ 
  if(n <= 0) return -1;
  int low = 0, high = n-1;
  while(low < high)
  {
    /*
    这里中间位置的计算就不能用low+((high-low)>>1)了，因为当low+1等于high
    且A[low] <= target时，会死循环；所以这里要使用low+((high-low+1)>>1)，
    这样能够保证循环会正常结束。
    */
    int mid = low+((high-low+1)>>1);
    if(A[mid] > target)
      high = mid-1;
    else // A[mid] <= target
      low = mid;
  }
  /* 
  循环过程中，当high小于n-1时，A[high+1]是大于target的，因为A[mid] > target时，
  high=mid-1；当low大于0时，A[low]是小于等于target的，因为A[mid] <= target时，
  low = mid；循环结束时，low 等于 high，所以，如果A[high](A[low])等于target，
  那么high(low)就是target出现的最大位置，否则target在数组中不存在。
  */
  if(A[high] != target)
    return -1;
  else
    return high;
}

question 1 : why we cannot use int mid = low+((high-low)>>1);
answer : suppose you have test case A = [1,2], target = 2

  • low = 0, high = 1, mid = 0
  • A[mid] = 1 < target = 2, so low = 0 again.
  • infinite loop.

insted of int mid = low+((high-low+1)>>1);, I would rather use int mid = high - ((high - low)>>1), which looks better.

so the code becomes like this : 

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
int searchLastPos(int A[], int n, int target)
{ 
  if(n <= 0) return -1;
  int low = 0, high = n-1;
  while(low < high)
  {
    /*
    这里中间位置的计算就不能用low+((high-low)>>1)了，因为当low+1等于high
    且A[low] <= target时，会死循环；所以这里要使用low+((high-low+1)>>1)，
    这样能够保证循环会正常结束。
    */
    int mid = high -  ((high-low)>>1);
    if(A[mid] > target)
      high = mid-1;
    else // A[mid] <= target
      low = mid;
  }
  /* 
  循环过程中，当high小于n-1时，A[high+1]是大于target的，因为A[mid] > target时，
  high=mid-1；当low大于0时，A[low]是小于等于target的，因为A[mid] <= target时，
  low = mid；循环结束时，low 等于 high，所以，如果A[high](A[low])等于target，
  那么high(low)就是target出现的最大位置，否则target在数组中不存在。
  */
  if(A[high] != target)
    return -1;
  else
    return high;
}

In fact, problme 2 is similar to the get_upperbound

Problem 3

given a sorted array, may contains duplicates, find a biggest i which makes A[i] < target, return i, if not, return -1.

problem 3 is ask for A[i] < target, problme 2 is aksing for A[i]=target, this is the difference.

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
int searchLastPosLessThan(int A[], int n, int target)
{
  if(n <= 0) return -1;
  int low = 0, high = n-1;
  while(low < high)
  {
    //int mid = low+((high-low+1)>>1); // 注意，不要导致死循环
        int mid = high - ((high - low)>>1);
    if(A[mid] < target) // 1
      low = mid; // 2
    else // A[mid] >= target // 3
      high = mid-1; // 4
  }
  /* 
  循环过程中，当low大于0时，A[low]是小于target的，因为A[mid] < target时，
  low=mid；当high小于n-1时，A[high+1]是大于等于target的，因为A[mid] >= target时，
  high = mid-1；循环结束时，low 等于 high，所以，如果A[low](A[high])小于target，
  那么low(high)就是要找的位置，否则不存在这样的位置（A[0] >= target时）。
  */
  return A[low] < target ? low : -1;
}

notice, code 1 2,3 and 4 is differnt from the above problem. need to be very careful.

Problem 4

given a sorted array, may contains duplicates, find a smallest i which makes A[i] > target, return i, if not, return -1.

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
int searchFirstPosGreaterThan(int A[], int n, int target)
{
  if(n <= 0) return -1;
  int low = 0, high = n-1;
  while(low < high)
  {
    int mid = low+((high-low)>>1); // 1
    if(A[mid] > target)  // 2
      high = mid; // 3
    else // A[mid] <= target // 4
      low = mid+1; // 5
  }
  /* 
  循环过程中，当low大于0时，A[low-1]是小于等于target的，因为A[mid] <= target时，
  low=mid+1；当high小于n-1时，A[high]是大于target的，因为A[mid] > target时，
  high = mid；循环结束时，low 等于 high，所以，如果A[high](A[low])大于target，
  那么high(low)就是要找的位置，否则不存在这样的位置（A[n-1] <= target时）。
  */
  return A[high] > target ? high : -1;
}

Problem 5

given a sorted array (non-descending), may contains duplicates, try to find out how many times target appears at the array. 

1
2
3
4
5
6
7
8
int count(int A[], int n, int target)
{
  int firstPos = searchFirstPos(A, n, target); // 第一次出现位置
  if(firstPos == -1)
    return 0;
  int lastPos = searchLastPos(A, n, target);  // 最后一次出现位置
  return lastPos-firstPos+1;  // 出现次数
}

there is also a similar problme in leet code : Search for a Range

Given a sorted array of integers, find the starting and ending position of a given target value.

Your algorithm’s runtime complexity must be in the order of O(log n).

If the target is not found in the array, return [-1, -1].

For example,
Given [5, 7, 7, 8, 8, 10] and target value 8,
return [3, 4]. 

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
class Solution {
public:
    vector<int> searchRange(vector<int>& nums, int target) {
        vector<int> res;
        if(nums.empty()) return res;
        res.push_back(get_lowerbound(nums, target));
        res.push_back(get_upperbound(nums,target));
        return res;
    }
    
    int get_lowerbound(vector<int> & nums, int target){
        int left = 0, right = nums.size()-1;
        while(left<right){
            int mid = left + (right-left)/2;
            if(target > nums[mid]){
                left = mid+1;
            }
            else{
                right = mid;
            }
        }
        return (left < nums.size() && nums[right] == target) ? right : -1;
    }
    
    int get_upperbound(vector<int> &nums, int target){
        int left = 0, right = nums.size()-1;
        while(left<right){
            int mid = right - (right-left)/2;
            if(target < nums[mid]){
                right = mid-1;
            }
            else{
                left = mid;
            }
        }
        
        return (right < 0 || nums[left] != target)  ? -1 : left;
    }
};